Mr Reece's Growing Post
I will be creating my own growing post over the next week based upon four questions that are similar to those that you received in class. I will be building upon this original post as we learn new information relating to the 4 questions that I will have to answer.
The Questions
1. What are pentominoes and how many unique pentominoes can we create?
What are pentominoes and how many unique pentominoes can we create?
2. Identify the pattern that is occuring in the following shapes and relate what is happening with the pattern with words.
3. Create a Algebraic function that describes what is occuring in this pattern.
4. Use this pattern to express what is happening with the 10th, 25th and 50th shape.
Question #1
A pentominoe is created when we join five identical congruent squares together to form a single shape. A square can only touch another square if both sides are aligned together so that the sides are perfectly equal to one another.
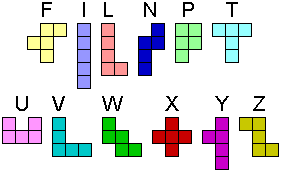 There are a total of 12 unique pentominoes that can be created using 5 equal sized squares. A pentominoe that is a reflection (flipped) or rotation of one of these 12 pentominoes is not considered unique.
There are a total of 12 unique pentominoes that can be created using 5 equal sized squares. A pentominoe that is a reflection (flipped) or rotation of one of these 12 pentominoes is not considered unique.
These are the 12 unique pentominoes (image taken from wikipedia)
I will answer question #2 tomorrow.
Mr. R
 Question #2
Question #2
Identify the pattern that is occuring in the following shapes and relate what is happening with the pattern with words.
ANSWER
Pattern #1 There are three different patterns here. For the first pattern we are slowly building a cross. In the original step we have a horizontal line of 3 blocks. In the next pattern we add 2 blocks vertically at the center area to create a cross. For step 3 we add more horizontal blocks, step 4 two vertical blocks etc. Each odd number adds two horizontal blocks, each vertical step 2 vertical blocks. Numerically the pattern is growing as 3, 5, 7, 9....
Pattern#2. This is pattern adds one additional row to the growing checkboard that is one tile larger than the last. The first row has 1 tile, the second row 2 tiles with a blank space between them, the third row 3 tiles with a blank space between each etc. Numerically the pattern is growing as 1, 3, 6, 10... (1, 1+2, 1+2+3, 1+2+3+4...)
Pattern #3. This pattern involves the construction of a pyramis using triangular shapes. Step 1 involves 1 triangle, step 2 FOUR small triangles joined to form 1 large triangle, step 3 NINE triangles joined to form 1 larger pyramid etc.
Numerically the pattern is 1, 5, 14, 30...
Question #3 Create a Algebraic function that describes what is occuring in this pattern.
Note: n = the shape or step 1
Pattern #1: 2n + 1 = the number of tiles that are needed for each step.
Pattern #2: n(n+1)/ 2
Pattern #3: n2
Question #4:Use this pattern to express what is happening with the 10th, 25th and 50th shape.
Pattern #1: 10th Position: 21, 25th position: 51, 50th postion 101
Pattern #2: 10th Position: 55, 25th position: 325, 50th postion 1275
Pattern #3: 10th Position: 100, 25th position: 625, 50th postion 2500
So here are my answers to the questions that I asked for my growing post. Your questions are different, and since a few people have already done their growing post look at what they have done and use it as a guide along with this post for what I expect.
Remember that these posts make up 30% of your grade for this unit (about the same as your test) so one or two word answers for each question is not sufficient.
Have fun everyone, enjoy the weekend and I will see you monday
Mr. R
The Questions
1.
 What are pentominoes and how many unique pentominoes can we create?
What are pentominoes and how many unique pentominoes can we create?2. Identify the pattern that is occuring in the following shapes and relate what is happening with the pattern with words.
3. Create a Algebraic function that describes what is occuring in this pattern.
4. Use this pattern to express what is happening with the 10th, 25th and 50th shape.
Question #1
A pentominoe is created when we join five identical congruent squares together to form a single shape. A square can only touch another square if both sides are aligned together so that the sides are perfectly equal to one another.
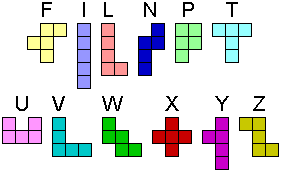 There are a total of 12 unique pentominoes that can be created using 5 equal sized squares. A pentominoe that is a reflection (flipped) or rotation of one of these 12 pentominoes is not considered unique.
There are a total of 12 unique pentominoes that can be created using 5 equal sized squares. A pentominoe that is a reflection (flipped) or rotation of one of these 12 pentominoes is not considered unique.These are the 12 unique pentominoes (image taken from wikipedia)
I will answer question #2 tomorrow.
Mr. R
 Question #2
Question #2Identify the pattern that is occuring in the following shapes and relate what is happening with the pattern with words.
ANSWER
Pattern #1 There are three different patterns here. For the first pattern we are slowly building a cross. In the original step we have a horizontal line of 3 blocks. In the next pattern we add 2 blocks vertically at the center area to create a cross. For step 3 we add more horizontal blocks, step 4 two vertical blocks etc. Each odd number adds two horizontal blocks, each vertical step 2 vertical blocks. Numerically the pattern is growing as 3, 5, 7, 9....
Pattern#2. This is pattern adds one additional row to the growing checkboard that is one tile larger than the last. The first row has 1 tile, the second row 2 tiles with a blank space between them, the third row 3 tiles with a blank space between each etc. Numerically the pattern is growing as 1, 3, 6, 10... (1, 1+2, 1+2+3, 1+2+3+4...)
Pattern #3. This pattern involves the construction of a pyramis using triangular shapes. Step 1 involves 1 triangle, step 2 FOUR small triangles joined to form 1 large triangle, step 3 NINE triangles joined to form 1 larger pyramid etc.
Numerically the pattern is 1, 5, 14, 30...
Question #3 Create a Algebraic function that describes what is occuring in this pattern.
Note: n = the shape or step 1
Pattern #1: 2n + 1 = the number of tiles that are needed for each step.
Pattern #2: n(n+1)/ 2
Pattern #3: n2
Question #4:Use this pattern to express what is happening with the 10th, 25th and 50th shape.
Pattern #1: 10th Position: 21, 25th position: 51, 50th postion 101
Pattern #2: 10th Position: 55, 25th position: 325, 50th postion 1275
Pattern #3: 10th Position: 100, 25th position: 625, 50th postion 2500
So here are my answers to the questions that I asked for my growing post. Your questions are different, and since a few people have already done their growing post look at what they have done and use it as a guide along with this post for what I expect.
Remember that these posts make up 30% of your grade for this unit (about the same as your test) so one or two word answers for each question is not sufficient.
Have fun everyone, enjoy the weekend and I will see you monday
Mr. R


0 Comments:
Post a Comment
<< Home