Add-in for Microsoft Word

If you click on this link it will bring you to a page where you can download an extension for Microsoft Word that allows you to create your post in word and then publish it to blogger. The installation takes under a minute to complete and to set up the addition to blogger all you have to do it enter your username and password under blogger settings.

Have fun using this great tool for word and blogger.

Mr. R

Algebra due dates

Along with your test on Tuesday June 6th, you have multiple items from our unit on Algebra which are due. They include

• All four growing posts
• All completed worksheets in your duotang, along with a title page. (I will post a list of all of the sheets that need to be completed.)
  
• 3-point Approach for Algebra
  

Getting your growing posts completed, and your duotang upto date will help you prepare for your test that day.

Happy blogging everyone!

Mr. Reece

Unit test in Algebra

Our Unit Test is set for Tuesday June 6.

I will be posting helpful online resources on Wednesday and Thursday to help you prepare for your final unit test. We will be spending classtime Wednesday and Thursday reviewing material to prepare next Tuesday.

Check my blog frequently over the next few days for all kinds of important information for the test.

Mr. Reece

Growing Post 4: Due June 6th

Question 1: Formulas. We’ve learned how to write algebraic equations in the form of

mx + b = y. Convert these two sentences into algebraic equations using the above formula.

Sentence 1: Scott is 2 years older than Donald who turns 12 on June 21^st 2006. Write this sentence in the format of mx + b = y, then convert it into an expression which allows us to figure out the age of Scott.

Sentence 2: Elizabeth has $200 in her savings account. She makes $40 every two weeks babysitting for her next door neighbours. If Elizabeth saves all of her money solve for how much money she will have in one year.

Question 2: Creation. You need to create two questions for your classmates that cover different concepts (ex: T-Charts, patterns, equations, graphs etc.) that you have learned in this unit on Algebra. You then need to show how to solve the questions. Your mark will be based upon the level of question’s difficulty, and the effort put into your answer.

Question 3: Reflection. You need to look back at the chart that we filled out during the first day of the unit. This is the chart where you coloured a topic red, yellow or green. You now need to pick one concept that you coloured yellow or red and reflect in words what new skill/idea that you have learned on this topic.

Question 4: Preparing for the final exam. You need to think about the year that has past in mathematics and decide which topic is your weakest, and what you need to learn during class review in order to prepare yourself for the final exam. It is not enough to say fractions, instead pick your weakest area of fractions, say the subtraction of fractions, and give an example of what you don’t understand.

This is our final week of Algebra, we will be starting our review for the final exam next week.

Growing Post Hall of Fame

Our math classes now have a place to celebrate the great growing posts that are being created by everyone. You can find the hall of fame here
If you wish to nominate any scribe posts please send me a comment telling me which post you believe deserves mention in the hall of fame.

Thanks everyone for your hard work

Mr. R

Growing Post for the week of May 15th to 20th (Due Tuesday May 23rd)

Question #1: Solve all 3 parts of the problem below

Jack collects baseball cards. Jack has 180 baseball cards in his collection. At the end of each month Jack buys 25 baseball cards to add to his collection.

a)Create a T-Chart showing how many baseball cards Jack has at the end of the next 4 months.

b)Create an algebraic formula based upon the problem above

c)If Jack just turned 8 years old this month and Jack continues to buy the same amount of baseball cards each month, how many baseball cards will jack have when he turns 12?

Question #2: Use the chart to figure out the questions below.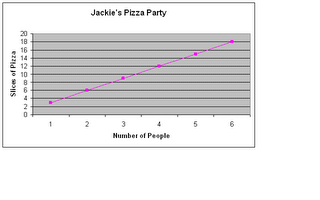

Jackie is planning on having a pizza party with some of her friends. She is trying to figure out how many pizza’s to order. She knows that each pizza has six slices of pizza.

a)If Jackie thinks that there will be four people at the party (counting herself) how many pizza’s should she order?

b)If two more people show up at the party how many more pizza’s does she need to order?

Question #3: Answer the questions below based upon this information

Kathy has $20 in her savings account. Each month she adds another $15 to her savings account. In order to calculate how much money she will have in one year Kathy has created this algebraic formula: 20 + 15n = Savings amount

a) Calculate how much money Kathy will have in one year

b) Suppose Kathy counted wrong and she really has $25 in her account instead of $20. Change the algebraic formula to reflect this miscalculation.

Question #4: Solve the following equations. Show all of the steps that are needed.

a) 3n + 4n + 7 = 2n + 12

b) 8n – (4 + 9) = 11

c) (8 – 3 )n + 7n + 8 = 4n + 40

Have fun with the growing posts everyone!

Growing Post Questions Due Monday May15th

Question #1: What is meant by the terms "Rotation Symmetry" and "Reflection Symmetry"? How does this relate to pentominoes? Explain these terms so that anyone who reads your post understands what you mean.

Question #2: Create a pattern. You must represent this pattern both pictorially (i.e. with a picture or diagram) and with numbers. You must show the first 4 steps of your pattern.

Question #3: Describe in words what is occuring with your pattern and if your pattern has an ending or if it continues on indefinately. Make sure that your explanation is clear enough that the person reading your description could understand your pattern without seeing your diagram.

Question #4: Create a T-Chart that shows what is happening with your pattern. You must show the first 4 steps of your pattern with the T-chart.


Remember if you are having problems with these answers use your friends and the internet to help you discover the answers to your questions.

Happy Posting everyone.
Mr. R

The growing post

The growing post.

So what you may ask is a growing post?
Well this is your chance to reflect and speak about what you have learned in class. It is a chance for you to share your throught and ideas on topics that we have covered in class.

Think of the growing post as a perfect way to check that you are learning what you need to know in class, and that you have tested your knowledge and are confident in what you have learned.

So how does the growing post work?
Every week you will be given questions in class that relate to the material that we will learn that week. During the week take a few minutes (10 to 15 max) to try to answer a question or two based upon the topics that we have covered in class. If you choose blogger as your medium for doing the growing post continue to add to the same post throughout the week. Do not create a new post for each addition to your post. If you choose paper and pen, make sure that you keep your growing post in your duotang as you must hand it in each Monday after class.

Examples of growing posts.
Mr. Harbeck's classes have been creating their own growing posts for the past few weeks. Here are examples of some of the best growing posts that his students have created.

Grade 8 Growing Post Hall of Fame
Check the right side of my blog for the link to the Grade 8 Growing Post Hall of Fame or click here

My Own Growing Post
I will construct my own growing post based upon knowledge that is learned this week around these unique 4 questions.

1. What are pentominoes and how many unique pentominoes can we create?

2. Identify the pattern that is occuring in the following shapes and relate what is happening with the pattern with words.

3. Create a Algebraic function that describes what is occuring in this pattern.

4. Use this pattern to express what is happening with the 10th, 25th and 50th shape.

I will answer these 4 questions throughout the week highlighting how to create the growing post here on my blog.

Mr. R

Mr Reece's Growing Post

I will be creating my own growing post over the next week based upon four questions that are similar to those that you received in class. I will be building upon this original post as we learn new information relating to the 4 questions that I will have to answer.

The Questions

1. What are pentominoes and how many unique pentominoes can we create?
2. Identify the pattern that is occuring in the following shapes and relate what is happening with the pattern with words.
3. Create a Algebraic function that describes what is occuring in this pattern.
4. Use this pattern to express what is happening with the 10th, 25th and 50th shape.



Question #1
A pentominoe is created when we join five identical congruent squares together to form a single shape. A square can only touch another square if both sides are aligned together so that the sides are perfectly equal to one another.

There are a total of 12 unique pentominoes that can be created using 5 equal sized squares. A pentominoe that is a reflection (flipped) or rotation of one of these 12 pentominoes is not considered unique.

These are the 12 unique pentominoes (image taken from wikipedia)

I will answer question #2 tomorrow.

Mr. R

Question #2
Identify the pattern that is occuring in the following shapes and relate what is happening with the pattern with words.

ANSWER
Pattern #1 There are three different patterns here. For the first pattern we are slowly building a cross. In the original step we have a horizontal line of 3 blocks. In the next pattern we add 2 blocks vertically at the center area to create a cross. For step 3 we add more horizontal blocks, step 4 two vertical blocks etc. Each odd number adds two horizontal blocks, each vertical step 2 vertical blocks. Numerically the pattern is growing as 3, 5, 7, 9....

Pattern#2. This is pattern adds one additional row to the growing checkboard that is one tile larger than the last. The first row has 1 tile, the second row 2 tiles with a blank space between them, the third row 3 tiles with a blank space between each etc. Numerically the pattern is growing as 1, 3, 6, 10... (1, 1+2, 1+2+3, 1+2+3+4...)

Pattern #3. This pattern involves the construction of a pyramis using triangular shapes. Step 1 involves 1 triangle, step 2 FOUR small triangles joined to form 1 large triangle, step 3 NINE triangles joined to form 1 larger pyramid etc.
Numerically the pattern is 1, 5, 14, 30...

Question #3 Create a Algebraic function that describes what is occuring in this pattern.

Note: n = the shape or step 1
Pattern #1: 2n + 1 = the number of tiles that are needed for each step.
Pattern #2: n(n+1)/ 2
Pattern #3: n²


Question #4:Use this pattern to express what is happening with the 10th, 25th and 50th shape.

Pattern #1: 10th Position: 21, 25th position: 51, 50th postion 101
Pattern #2: 10th Position: 55, 25th position: 325, 50th postion 1275
Pattern #3: 10th Position: 100, 25th position: 625, 50th postion 2500


So here are my answers to the questions that I asked for my growing post. Your questions are different, and since a few people have already done their growing post look at what they have done and use it as a guide along with this post for what I expect.

Remember that these posts make up 30% of your grade for this unit (about the same as your test) so one or two word answers for each question is not sufficient.

Have fun everyone, enjoy the weekend and I will see you monday

Mr. R

Sunday night math games

Since I didn't post a Sunday night math game last week I figured that I'd make up for it by posting two games this weekend.

The first game is the problem solving game Sodoku that many of your have attempted in class. Click Here to go and play this challenging number puzzle game.





The second game is called Cubis. The goal is to remove blocks of the same colour in groups of three or more. While it sounds simple it will keep you busy for hours if you let it.

Have a great night everyone

Mr. Reece

Week of May 8th to 12th

This week we are starting our final unit of the year, dealing with the wonderful concept of Algebra.

We will be focusing upon multiple areas within the area of algebra from pattern recognition and building to the creation of T-Charts and graphs to help us understand what is occuring in the pattern to finally the creation of our own algebric formulas in order to describe what is occuring in our patterns using concrete language.

Another goal is that we will spend time each day learning how to talk and write about math. We have not in my opinion been spending enough time writing about math and what is happening in our learning.

Finally we will be integrating blogger more closely into this final unit with a concept called the growing post (it will act as a reflection piece for what we are learning in class.) This growing post will be worth a significant portion of this unit's marks so it will be wise to either spend time on blogger during the week or be prepared to create your growing post on paper and keep safe care of it over the next 3 to 4 weeks.

This unit promises to be plenty of fun so be prepared to challenge your mind these next few weeks everyone!

See you on Monday.

Mr R.